トレーニング指導者のためのパフォーマンス測定と評価#20 曲線スプリント
2024/11/08
曲線スプリントの理論と実践
球技スポーツにおける曲線スプリントテストとトレーニング
記事はJATI EXPRESS No.103に掲載のものです。
【概要】
・球技スポーツにおけるスプリントの大半は直線ではない
・曲線スプリントテストとその活用
・曲線スプリント能力は曲線スプリントトレーニングでのみ向上する
・曲線スプリントにおける内側脚と外側脚
・曲線スプリント能力向上のためのトレーニング
球技スポーツではそのスプリントのほとんどは曲線を描いて行われている。にもかかわらず、これまでスプリントテストやスプリントトレーニングはほとんど直線だけで行われてきた。曲線を走るほうが多いのに、測定やトレーニングは直線がほとんどというのは考えてみればおかしなことだ。曲線スプリントについての研究もわずかしかない。そこで、今号では、「球技スポーツにおける曲線スプリントテストとトレーニング」について解説する。
1.球技スポーツにおけるスプリントの大半は直線ではない
スポーツにおいて曲線を走ることは、陸上競技の200mを超えるトラック種目だけではありません。球技スポーツではそのスプリントのほとんどは曲線を描いて行われています。
例えば、ラグビーやアメリカンフットボールのコーナーぎりぎりのインゴールやエンドゾーンを攻めるとき、サッカーのタッチライン沿いからのオーバーラップ、スルーパスを受けるためにいったんインサイドからアウトサイドに流れながら再びゴールに向かいながらボールに追いつく場面、バスケットボールにおけるカットインあるいはドライブやペネトレイトと呼ばれるゴールに向かうプレイ等々では容易にその場面を見ることができます。
ある2点間の最短距離は直線ですが、スプリントの開始から目標に対して直線的に最短距離を走るのではなく、走っている最中に目標の位置や周辺の状況が変化する場合、できるだけブレーキをかけずに加速しながらあるいは速度を維持しながら徐々に角度を連続的に変えていく必要がある場合にスプリントは曲線を描きます。
にもかかわらず、これまでスプリントテストやスプリントトレーニングはほとんど直線だけで行われてきました。曲線を走るほうがむしろ多いのに、測定やトレーニングは直線がほとんどというのは考えてみればおかしなことです。曲線スプリントについての研究もわずかしかありません。
従来、一直線のスプリントだけではなく方向転換走も行われてきましたが、そのほとんどはプロアジリティーやスリーコーンテストやTテストに代表されるように、直線的なスプリントの反復と急激な方向転換であり、最大スピードで全力走をしている部分は直線です。
球技スポーツにおけるスプリントの特異的な能力を評価し、課題を発見し、適切なトレーニングを実施するめにはこの曲線スプリントに焦点を当てたテストやトレーニングが必要となります。
(1)サッカーにおける曲線スプリント
イングランドプレミアリーグの10試合にについて、最大速度でのスプリントを調べた結果、ポジションによって多少異なりますが、その83-88%が曲線走であることが示されています1)。
また、U18のイングランド・プレミアリーグの選手13名(17.5±0.7歳)を対象に、6試合中の時速24㎞を超えた全873本のスプリントについて、GPS(GNSS)から得られたXY座標上の連続的なデータを用いて、そのスプリント角度の大きさを分析するという研究が行われました2)。
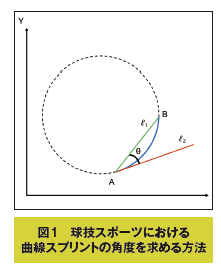
どうやってスプリント角度を調べたか、それは次のような方法です。図1の青い曲線で示したように、曲線スプリントの軌跡は円の一部である弧であると仮定し、次にスプリントの開始地点Aと終了地点Bを結ぶ直線ℓ₁をこの弧の弦(緑の直線)として、この弦という直線ℓ₁と、スプリント開始点における弧の接線(赤の直線)ℓ₂という2本の直線のなす角度をスプリント角度(θ)と定義しました。そして、ℓ₁とℓ₂のそれぞれのXY座標軸上の傾き(タンジェント)を求め、そこから傾きが既知の2つの直線のなす角度を求めるために、タンジェントの加法定理を用いてθを計算し、これを曲線スプリント角度としました。
その結果、全スプリントの約60%が曲線走であり、その本数や距離は、ポジションによって異なりますが、フォワードがもっと多く1試合平均21本で平均距離は12.2mでした。最も少ないセンターミッドフィールダーで9本、平均距離は12.5mでした。曲線スプリント角度は平均で約5°でしたが、センターフォワードは他のポジションに比べて10~15°、あるいは15°以上のスプリントが多く、最大30°という大きな角度にまでおよぶことが確認されました。
(2)ラグビーのフルバックにおける曲線スプリント
これと同じ方法でオーストラリアのセミプロフェッショナルU20の男子ラグビーチームに所属する2名のフルバックの選手を対象とし、4試合から時速24km以上の54本のスプリントが分析されました3)。その結果、全スプリントの68.5%に相当する37本が曲線スプリントであり、曲線スプリントの平均角度は10.44°、平均距離は20.8mでした。0~5°および5~10°がそれぞれ17本と最も多いのですが、10~15°が8本、15~20°も5本あり、さらに40°以上という大きな角度での40mを超える曲線スプリントが2本あり、全体的にみてもサッカーよりも角度が大きめで距離も長い傾向が示されました。
これはラグビー競技におけるフルバックというポジション特性を反映したものと思われ、同じラグビーにおいても中央で短い距離の加減速を繰り返すフォワードであれば違った結果になったであろうと考察されています。
(3)バスケットボールにおける曲線スプリント
イタリアの女子プロバスケットボール5試合(セリエA1の3試合とヨーロッパリーグ2試合)についてビデオ映像からの分析の結果、全スプリントの80%以上は10m以下で、1~5mのスプリントが最も多く約57%でした。そのうち直線が48.3%、曲線が31%、方向転換走が20.7%でした。また曲線スプリントのうち59.1%はボールを保持してのものでした4)。
2.曲線スプリントテストとその活用
このように、球技スポーツにおけるスプリントの大半は曲線であることは明らかです。この事実に基づいて、現場でできるだけ簡単に選手の曲線スプリント能力を測定し評価するために新たに開発されたテストを紹介します。
(1)サッカーのための曲線スプリントテストの開発
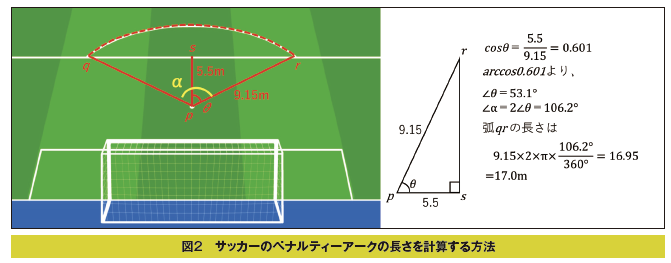
まず、サッカー用に開発されたテストです5)。サッカーの競技場に示されたFIFAのルール通りのライン表示をもとにペナルティーアーク(Dとも呼ばれる弧)の長さを求めると次のようになります(図2)。
ペナルティーアークは、ペナルティーマークpを中心として半径9.15mで作られる円がペナルティエリアのラインと交わる左右の点qとrで切り取られた弧の長さですから、弧の中心角αがわかれば、αの360°に対する割合で計算できます。
ペナルティーマークからペナルティエリアの端までの直線距離は5.5mなので、図の右側の式に示したように、三角形prsは、∠θの直角三角形となります。斜辺と隣辺の長さがわかっているので、三角関数cosθを求めると0.601となり、ここから逆三角関数arccosθを求めると∠θは53.1°であることがわかります。∠αはこの2倍ですから、半径9.15mの円周に対する中心角αの弧の長さは16.9m≒17mだということになります。
三角形prsの3辺のうち斜辺と一方の辺の長さがわかっていますから、三平方の定理によって直線srの長さを求めると7.31mとなり、弧qrに対する弦の長さはその倍の14.62mとなりますから、弦長=2×半径×sin(θ/2)から中心角が計算できそこから弧の長さを求めることもできます。
このように、公式ピッチのペナルティーアークの曲線が17mであることが明確ですので、弧のスタート地点とゴール地点に光電管を設置すれば17mの曲線スプリントタイムをいつでも簡単に計測することができます(図3)。
走る方向を変えることで得意な方向(速い側)と苦手な方向(遅い側)を見つけることもできます。また、弧の中央にもう1つ光電管を置けば、8.5mのスプリットタイムを計測でき、スタート能力と加速能力を識別することもできます。
(2)サッカー選手における曲線スプリント能力
セミプロ選手の場合
このようなセッティングでスペインの2部および3部リーグに所属するセミプロの男子サッカー選手(22±3.32歳)40名を対象にタイミング計測機器Wittyを用い、曲線スプリントの左および右方向で48時間を隔てて2回測定が行われました5)。その結果、級内相関係数(ICC)が右方向で0.89、左方向で0.93という非常に高い値が示され、また変動係数(CV)は右方向が0.87%、左方向が1.15%という低い値が示されました。このことから、この曲線スプリントテストは高い信頼性を持つテストであるということが言えます。
また、この研究では曲線距離と同じ17mの直線スプリントが比較されました。その結果、直線スプリントタイムと曲線スプリントタイム間の決定係数(R²)は、左右のうち速いタイムを出した側で34%、遅いタイムを出した側で37%でした。このことから高い直線スプリント能力を有する選手が必ずしも曲線スプリントにおいても高い能力を持つとは限らないということが言えます。さらに、速い側と遅い側のタイムの相関係数(r)は非常に強く0.88であり、一方の方向で優れた曲線スプリント能力を持つ選手はもう一方の方向でも優れた能力を持つことが示されました。これらのことから、このテストで測定される曲線スプリント能力と直線スプリント能力は異なる身体的な特質を示すものであり、それぞれ別のものとして評価されトレーニングされるべきものであるということができます。
女子トッププロ選手の場合
ブラジルのナショナルチームメンバー8名を含む17名の女子トッププロサッカー選手を対象に、同様の17m曲線スプリントテストと17m直線スプリントテストが行われました6)。その結果、両者の間には、速い側でr=0.95、遅い側でr=0.93というほぼ完全な相関関係が示されました。このデータから判断すれば、直線スプリント能力の高い選手は曲線スプリント能力においても高い能力を持つということになります。
U20エリート選手の場合
スペインの1部リーグに所属するU20のエリート男子サッカー選手(18.5±0.5歳)28名を対象とした研究7)では、直線スプリントタイムと曲線スプリントタイムの早い側でr=0.82、遅い側で0.74という高い相関係数が示され、この結果からも直線で優れたスプリント能力を持つ選手は曲線においても優れたスプリント能力を持つ可能性が高いと言えます。
(3)曲線スプリント能力と直線スプリント能力の関係
最初に示した成人セミプロのデータによれば、直線スプリントと曲線スプリントは別の能力であるということが考えられましたが、女子のトッププロの結果とU20のエリート選手の結果を見ると、直線スプリントに優れた選手は曲線スプリントにおいても高い能力を示すということになります。この違いはおそらく選手のレベル差(セミプロとエリート)によるものと考えることができます。
上述の研究7)では、曲線スプリントテストによって得られた値と同じ距離の直線スプリントテストの結果を比較することで、「曲線スピード不足値」という指標を算出しています。17m直線スプリント速度―17m曲線スプリント速度というシンプルな式で求められる数値で、この数値が大きければ大きいほど直線スプリントで出せるスピードに比べて曲線スプリントで出せるスピードが劣ることになり、この数値が小さければ小さいほど、曲線であっても直線に近いスピードが出せるということを意味します。
この曲線スピード不足値は、曲線スプリントにおける速い側のスピードと負の相関を示したことから、速い側では直線スピードをうまく使えていることが考えられました。また、この曲線スピード不足値と直線スプリント速度との関係を見たところ、遅い側の曲線スプリント不足値の大きさと直線スプリント速度の間には高い相関がありましたが、速い側では直線スプリント速度との相関は示されませんでした。このことは、曲線スプリントの速い側というのは、その人の直線スプリント速度に関係なく、直線スプリントに近い値で走れることができるが、曲線スプリントの遅い側では、直線スプリントの速度をうまく生かせてないことを意味します。したがって、曲線スプリントの遅い側の曲線スプリントを集中的にトレーニングすることによって、苦手な方向での曲線でも自信を持ってより効率よく走るためのメカニズムの向上を目指せる可能性があります。
(4)バスケットボールのための曲線スプリントテスト
上述したようにバスケットボールにおいても試合中のスプリントは決して直線ばかりではなく、その1/3は曲線であるという事実を背景として、公式のコート上に引かれた既存のスリーポイントラインを利用した曲線スプリントのテストも開発されています8)。
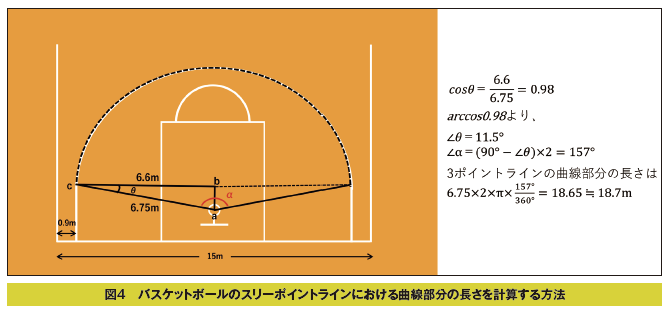
FBAルールによるバスケットボールのスリーポイントラインは、ゴールの中心から6.75mの半径で引かれた円の両端がサイドラインから0.9m内側にサイドラインと並行に引かれた直線と交わるように引かれています。したがって曲線部分が終わる点cからエンドラインと並行に引いた線が、ゴールの中心aからエンドラインに対して垂直に引いた直線と交わる点bまでの長さは、15m÷2-0.9m=6.6mとなり、直角三角形abcにおける∠θの大きさは、cos6.6/6.75=0.98ですから、逆三角関数arccos0.98から11.5°であることがわかります。すると直角三角形abcのもう一方の鋭角の大きさは78.5°ですから、スリーポイントラインの弧の中心角はその倍の157°となります。したがって、その360°に対する割合から、半径6.75mの円周全体に対する割合を求めると、スリーポイントラインの曲線部分の長さは18.65m≒18.7mであると計算されます(図4)。
バスケットボール選手の曲線スプリント能力
この曲線を用いてスペインの国内リーグのクラブに所属する14~17歳の男女30名を対象に行われた研究8)ではWitty光電管の他に、室内のローカルポジショニングシステム(LPS)も用いられました。その結果、スリーポイントラインを用いた曲線スプリントテストには高い妥当性と信頼性のあることが確かめられ、曲線スプリントは直線スプリントとは異なる加速特性と速度特性のあることが示されました。このことから、3ポイントラインを用いた曲線スプリントテストは、バスケットボール選手の曲線スプリント能力を評価するための妥当性のあるテストとして利用することができると言えます。
3.曲線スプリント能力は曲線スプリントトレーニングでのみ向上する
U16の男子サッカー選手(15.6±0.5歳)19名を対象に、直線スプリントトレーニングだけを行うグループと曲線スプリントトレーニングだけを行うグループに分けて、週2回6週間のスプリントトレーニングを実施する研究が行われました9)。
グループの違いは走るコースが直線か曲線かというだけで距離はどちらも17mとし、曲線スプリントはペナルティーアークを用いて、右回りと左回りで行われました。どちらのグループにおいても、全力でのスプリントを反復回数もセット数もレストタイムも完全に等しくなるようにコントロールされました(例えば17m×5本×2セット、レップ間レスト2分、セット間レスト5分)。その結果、直線スプリントトレーニング群は、10m、15m、20m、30mの直線スプリントにおいて、曲線スプリング群よりも統計的に有意に大きな改善を示しましたが、17m曲線スプリントテストでは曲線スプリント群にのみ有意な改善が示され、直線スプリントトレーニング群には有意な改善が見られませんでした。このことから、曲線スプリントスピードを改善させるためには曲線スプリントトレーニングが必要であることが示唆されます。
4.曲線スプリントにおける内側脚と外側脚
曲線スプリントでは、少なくない選手が右回りと左回りで得意な方向と苦手な方向を持っています。右回りと左回りでは、曲線の内側となる脚と外側になる脚が逆になりますが、内と外では何が違うのでしょうか。これを調べるために9名のスペインのセミプロサッカー選手(23±4.12歳)を対象に17mの直線スプリントとペナルティーアーク上の曲線スプリントが比較されました10)。
直線スプリントにおける接地時間と曲線スプリントの接地時間を比較したところ、曲線スプリントにおいて外側となる足の接地時間は直線スプリントにおける接地時間と有意な差がありませんでしたが、内側の足の接地時間は有意に長くなることが示されました。
また、曲線スプリントにおいて得意な方向(速い側)と苦手な方向(遅い側)で内側と外側の接地時間の差を調べたところ、内側の足の接地時間が、得意な方向では苦手な方向よりも短いことが示され、外側の足の接地時間には得意な方向と苦手な方向に差は見られませんでした。したがって、得意な方向での曲線スプリントにおいては、回転の内側となる足の接地時間を短くすることでより速いスプリントスピードを得ていると推測できます。
さらに筋電図を見てみると、直線スプリントでは左右の脚で有意な筋活動の差は示されませんでしたが、曲線スプリントの外側脚と内側脚では差があり、外側脚で大腿二頭筋と中殿筋により高い筋活動が示され、内側脚では半腱様筋と内転筋群により高い筋活動が示されました。
このことから、内側脚では股関節内転と内旋モーメントが優勢となり、外側脚では股関節外転と外旋モーメントが優勢となると考えられ、この研究の著者らは、外側脚がいわば「連続的なサイドステップ」運動をしているのに対して、内側脚は「連続的なクロスステップ」運動をしているとも言えると述べています。
したがって、曲線スプリントにおけるこの内側脚と外側脚の異なる役割を踏まえたトレーニング戦略が必要になると考えられます。
5.曲線スプリント能力向上のためのトレーニング
(1)曲線スプリントにおける距離と半径と角度
ドイツのプロサッカークラブのU19チームに所属する男子サッカー選手(18.6±0.6歳)19名を対象として、曲線スプリントの弧の距離は等しく17mとしつつ、半径の長さだけを7.15m、9.15m、11.15mというように3種類で行ったスプリントテストが比較されました11)。その結果、すべてのスプリントタイムの間には非常に高い相関(r=0.79~0.91)が示されましたが、半径11.5mと半径7.15m、半径9.15mと半径7.14mの間で有意なタイム差が示され、半径が短いほどタイムが遅くなりました。
このことから、スプリント距離が同じであれば、半径が短いほうがタイムが遅くなることがわかります。その理由は弧の距離が同じであれば、半径が短いほうが曲線スプリントの角度が大きくなるという関係があり、スピードが一定であっても角度が大きいほど身体に対する強度が高くなるからです。
したがって、トレーニングの量と強度を考慮したプログレッションを踏まえて、実際に曲線スプリントのトレーニングを計画するためには、距離と角度の両方を考慮する必要があり、距離と角度の実際の競技場面との類似性も考慮する必要があります。
(2)曲線スプリントコースの設定法
これを適切に行うためのトレーニングのセッティングでは、半径を決めて弧を描き(メジャーの片端を円の中心として固定しもう片方をピンと引っ張ったまま円を描くように歩きながらマーカーを適当な一定間隔で並べる)、スタートからゴールまでの弦の距離(直線)を決めることで、実際に走る曲線部分の距離を設定します。
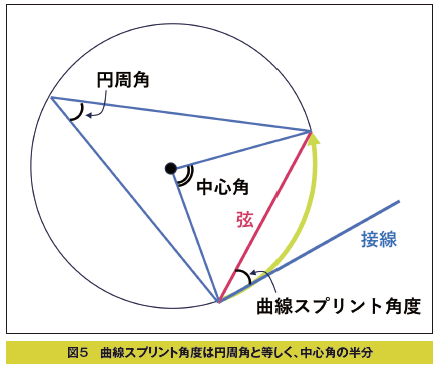
曲線スプリントの角度を、図1で示したように、弧のスタート地点の接線と弦という直線が作る角度で設定すると、図5に示したように、「接線と弦が作る角度の大きさは、その弦に対する円周角の大きさに等しい」とする接弦定理と、「1つの弧に対する円周角の大きさは一定であり、その弧に対する中心角の半分である」とする円周角の定理から計算することができます。
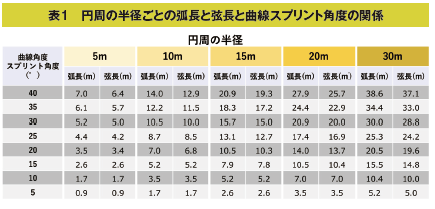
表1に、計算サイト12)から求めたいくつかのパターンをまとめています。
たとえば、同じ約10mという曲線距離を走りたい場合、半径が30mであれば角度は10°ですが、半径20mであれば15°、半径15mだと20°、半径10mだと30°というように半径を短く取ると曲線スプリント角度が大きくなります。
逆に角度を一定の例えば15°に固定してトレーニングしたい場合、半径5mの円周でコースを作ると曲線距離は2.6m、半径10mでは5.2m、半径15mで7.9m、半径20mでは10.5m、半径30では15.5mというように距離が長くなります。
これを基に、競技特性やポジション特性を考慮して、曲線スプリントの能力特性を比較したり、トレーニングにおける量と強度のプログレッションを合理的に計画したりすることができます。
(3)より高度な曲線スプリントテストとトレーニング
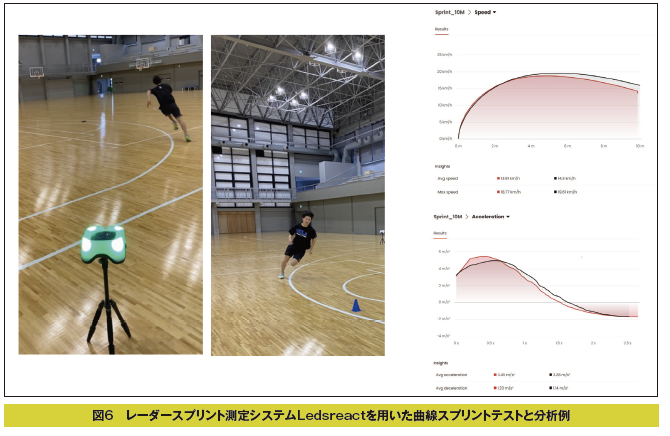
図6は、レーダーテクノロジーを用いた最新のスプリントスピード計測システムLedsreact(レッズリアクト)を用いて実施したバスケットボールの3ポイントライン上での曲線スプリントテストの様子とその分析例です。Ledsreactは選手にレーダーを照射することによって身体全体を追跡しタイムやスピードを計測します。距離を測って光電管を何台も設置しなくても、写真のように、本体1台だけで40mまでのスプリントやアジリティー運動を区間のタイムや平均スピードだけではなく、移動運動の連続的なスピードの変化を捉えグラフ化します。この例では、バスケットボールの曲線スプリントで頻出する距離のうち最も長い10mスプリントテストを行いました。
データは2回のスプリント結果をオーバーラップ表示しています。どちらも後半には減速しています。赤く示された試行では後半の5m以降の減速が大きいですが、下の加速度のグラフを見ると前半の加速は大きいことがわかります。
おわりに
以上のように、球技スポーツにおいては、直線だけではなく、競技特性を踏まえた曲線スプリントテストによる評価とトレーニングを進めていくことが必要です。ぜひお試しください。
参考文献
1. Caldbeck. P. Contextual sprinting in football [Doctoral thesis]. Liverpool John Moores University. 2010.
2. Fitzpartic JF., Linsley A., and Musham C. Running the curve: a preliminary investigation into curved sprinting during football match-play. Sport performance and science report. 2019, 55(1).
3. Hao Nian. From the Field - Case Study | Curvilinear running demands for a fullback in Rugby League. Journal of Australian Strength and Conditioning. 2021. 29(1).
4. Conte D., Favero TG., Lupo C., Francioni FM Capranica L., and Tessitore A. Time-motion analysis of Italian elite women’s basketball games: individual and team analyses. Journal of strength and conditioning research. 2015, 29(1), 144-150.
5. Filter A., Olivares J., Santalla A., Nakamura F. Loturco I., and Requena B. New curve sprint test for soccer players: Reliability and relationship with linear sprint. Journal of sports science. 2010, 38, 11-12.
6. Kobal R., Freitas TT., Filter A., Requena B., Barroso R., Rossetti M., Jorge RM., Carvalho L., Pereira L., and Loturco I. Curve sprint in elite female soccer players: Relationship with linear sprint and jump performance. International journal of environmental research and public health. 2021, 18, 2306.
7. Ioturco I., Pereira LA., Filter A., Orivares-Jabalera J., Reis VP., Fernandes V., Freitas TT., and Requena B. Curve sprinting in soccer: relationship with linear sprints and vertical jump performance. Biology of sport. 2020, 37(3), 277-283.
8. Baena-Raya, A, Díez-Fernández, DM, López-Sagarra, A, Martínez-Rubio, C, Soriano-Maldonado, A, and Rodríguez-Pérez, MA. Novel curvilinear sprint test in basketball: reliability and comparison with linear sprint. Journal of strength and conditioning research. 2023, 37(9), e535-e540.
9. Solleiro-Duran D., Cidre-Fuentes P., Rey E., Baena- Raya A., Filter A., and Padron-Cabo A. Effect of linear versus curvilinear sprint training on multidirectional speed in young soccer players: a randomized parallelgroup trial. Biology of sport. 2025, 42(1), 89-97.
10. Filter A., Olivares-Jabalera J., Santalla A., Morente- Sanchez J., Robles-Rodriguez J., Requena B., and Loturco I. Curve sprinting in soccer: Kinematic and neuromuscular analysis. International journal of sports medicine. 2020, 41, 1-7.
11. Altmann F., Ruf L., Filter A., Härtel S., Naujoks T., Rauprich M., Seyler C., Baydoun H., and Woll A. Curved sprinting in soccer: The influence of radius. International Journal of Sports Science & Coaching. 2024, 19(3),1234-1239.
12. このサイトでは弧長、弦長、半径、中心角のうち既知の2つを 入力すれば全てを自動的に計算してくれるので、オリジナルな テストの作成やトレーニング計画を立てるうえで便利です。 https://keisan.casio.jp/exec/user/1329041462
曲線スプリントの計測に:タイム計測システムWITTY